Efectul Dzhanibekov
Astăzi ceva din domeniul fizicii pentru curioși: Efect Dzhanibekov, cunoscută și sub numele de teorema rachetei de tenis, explică o instabilitate a corpurilor rotative cu trei momente diferite de inerție. Momentul de inerție indică rezistența unui corp la modificările mișcării de rotație a acestuia. Depinde de axa de rotație particulară și de geometrie. Înțelegerea dinamicii sistemelor clasice hamiltoniene este încă un obiectiv crucial cu o multitudine de aplicații care depășesc cu mult descrierea lor matematică. În cazul sistemelor integrabile cu câteva grade de libertate, o abordare eficientă se bazează pe o analiză geometrică pentru a caracteriza proprietățile dinamice ale sistemului mecanic. Astfel de fenomene geometrice sunt de obicei originea robusteții anumitor efecte care pot fi observate experimental. unul dintre ei este așa-numitul. Efect Dzhanibekov sau numit și efectul de rachetă de tenis.
Efect Janibekov în imponderabilitatea ISS
O derivare teoretică excelentă și detaliată a fenomenului poate fi găsită aici (https://arxiv.org/pdf/1606.08237.pdf). Avem de-a face aici cu unul care este puțin mai aspru, dar care explică totuși fenomenul. Din păcate, aici este necesară o anumită cunoaștere a dinamicii corpurilor rigide:
Luați în considerare o matrice de inerție (diagonalizată) cu momente de inerție I1 și I2 și I3 astfel încât I1 este cel mai mic și I3 este cel mai mare. Acum ia în considerare mișcarea în jurul axei momentului principal de inerție I3. Vectorul vitezei unghiulare este:
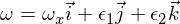
unde epsilonii sunt mici perturbații în celelalte două axe principale. Dacă acum introduceți acest lucru în ecuațiile Euler, veți obține:
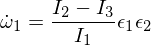
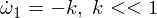
Acum diferențiem a doua ecuație a lui Euler:
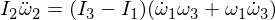
Înlocuirea omega 1 și omega 3 în expresia noastră și, din moment ce înmulțirea epsiloniilor, le face suficient de mici pentru a le ignora,
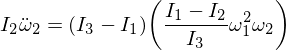
Acest lucru ne oferă o ecuație diferențială pentru Omega 2 de forma:
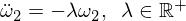
Soluția de bază este:
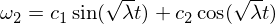
Prin urmare, știm că tulburarea de rotație din axa omega-1 este stabilă și face mișcări periodice, sau în terminologia mișcării rigide a corpului, că face o precesiune. Tulburarea omega 3 urmează un argument similar cu cele de mai sus și o voi lăsa ca un exercițiu pentru ca tu să treci prin ea. Pentru axa intermediară avem:
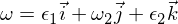
Inserat în ecuațiile Euler:
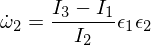
Diferențierea celei de-a treia ecuații a lui Euler dă:
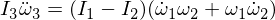
Să înlocuim expresiile noastre derivate:
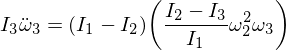
Acum rearanjați și obțineți următoarea ecuație diferențială:
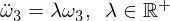
Observați că coeficientul este acum pozitiv, ceea ce duce la soluții exponențiale:
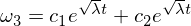
Această soluție arată că omega 3 este instabil de-a lungul axei intermediare, cu o perturbare a omega 2!
Ce înseamnă acest lucru?
Acum putem combina tot ceea ce am derivat și învățat pentru a înțelege teorema. Pur și simplu: dacă rotația de-a lungul axei intermediare este perturbată, rezultă o ecuație diferențială cu soluții exponențiale. Aceasta duce la o mișcare instabilă, spre deosebire de mișcarea precisă observată în celelalte două axe. Acest rezultat este destul de surprinzător. Nu există suport intuitiv pentru o astfel de teoremă, deoarece nu ne putem imagina de ce momentul intermediar de inerție ar duce la o rotație instabilă. Se pare că are un caracter pur matematic.